병합 정렬이란?
병합 정렬은 나누고 붙이는 과정을 기반으로 한 정렬 알고리즘이다. 하나의 배열을 둘로 나누고, 이를 정렬하여 다시 붙이게 된다.
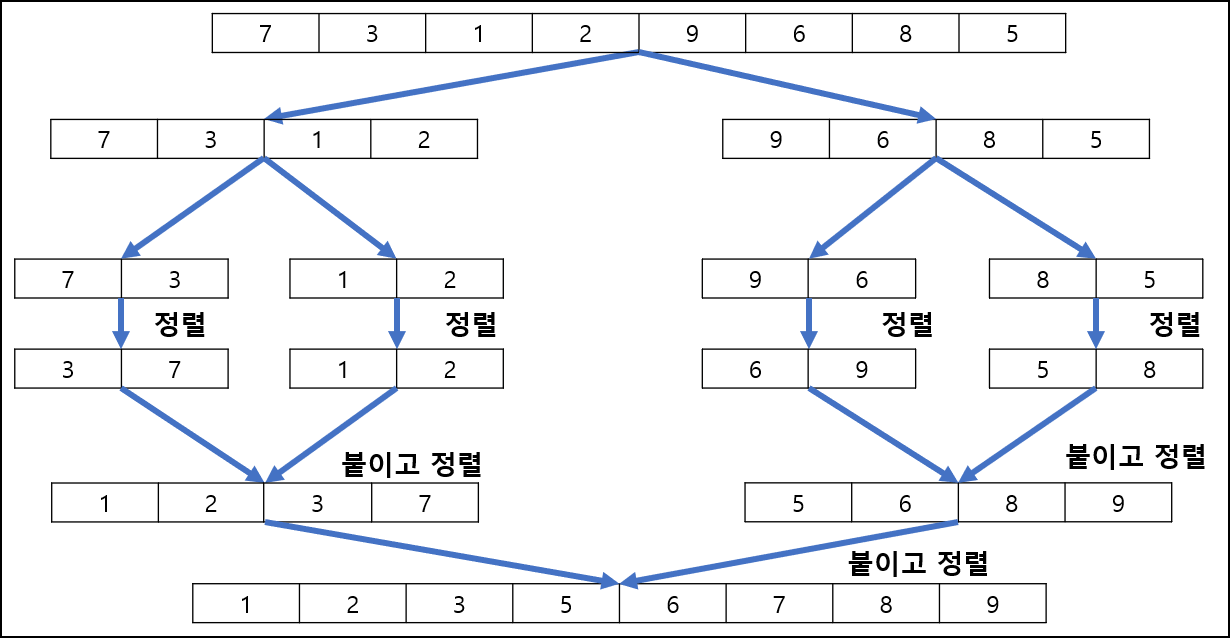
병합 정렬은 재귀 함수 호출로 정렬할 수 있는 데, 배열을 1/2씩 최대한 쪼갠 후 쪼개진 배열을 정렬하고, 최대한 쪼개진 배열을 둘씩 붙이고, 다시 정렬하고, 다시 붙이고...를 반복한다. 사실 설명보다 아래 그림을 이해하는 편이 더 쉽다.
이 정렬 방식은 최악, 최선 어느 경우에도 O(Nlong(N))의 시간 복잡도를 가진다.
공간 복잡도는 O(n)이다.
코드 부분 부분 해설
코드는 아래와 같은 형식으로 풀 수 있다.
1. 반으로 최대한 쪼갤 수 있을 때까지 쪼갠다. (재귀 함수 호출, 더 쪼갤 수 없을 때는 리턴)
2. 정렬의 가장 왼쪽을 가리키는 값(p1), 정렬의 중간 가리키는 값(p2), 가장 오른쪽을 가리키는 값(p3)을 지정한다.
3. p1과 p2를 비교하고 p3에 넣고, p1과 p2 중 사용된 값은 한 칸 오른쪽으로 이동한다. p3도 한칸 오른쪽으로 이동한다. 아래를 보면서 이해해 보자.
1번 '반으로 최대한 쪼갤 수 있을 때까지 쪼갠다'부터 살펴보자.
lt는 배열의 가장 왼쪽을 가리키도록, rt는 배열의 가장 오른쪽을 가리키도록 입력된다.
만약 가장 왼쪽과 가장 오른쪽 값이 같다면 더 이상 쪼갤 수 없다는 의미가 된다.
하나의 배열이 왼쪽 반, 오른쪽 반으로 쪼개지므로 DFS(lt, mid), DFS(mid+1, rt)로 선언한다.
void DFS(int lt, int rt)
{
if (lt<rt)
{
DFS(lt,mid);
DFS(mid+1,rt);
}
}
2. 정렬의 가장 왼쪽을 가리키는 값(p1), 정렬의 중간 가리키는 값(p2), 가장 왼쪽을 가리키는 값(p3)을 지정한다.
정렬 내의 값들을 비교하여 임시 정렬에 넣을 것이다. 이때 p1과 p2는 정렬 내의 두 값을 비교할 때 사용되고, p3는 임시 정렬 어디에 넣을지 가리키는 변수이다. 어떻게 정렬하는지는 아래에 그림으로 살펴보자.
3. p1과 p2를 비교하고 p3에 넣고, p1과 p2 중 사용된 값은 한 칸 오른쪽으로 이동한다. p3도 한칸 오른쪽으로 이동한다.
아래를 유심히 읽어보면 도움이 될 듯.
- p1과 p2 값을 비교한다.
- p2 값이 더 작으므로 p2가 가리키는 1이 p3의 위치에 들어간다.
- p1은 가만히 있고 (쓰이지 않았으므로) p2는 한 칸 오른쪽으로 이동한다.
- p3도 한 칸을 채웠으니 한칸 오른쪽으로 이동한다.
p1 값은 중간까지만 도달할 수 있고, p2값은 중간부터 배열 마지막까지 도달할 수 있다.

그런데, 잘 생각해보자. 반반 나누어 비교하는 것이기 때문에 p1값은 중간까지만 도달할 수 있다. p2는 중간부터 배열 마지막까지만 도달할 수 있다.
예를 들어 p1 쪽이 모두 작아서 p2는 전혀 움직이지 않았다면? 나머지를 또 temp 배열에 쓸어 담아 줄 코드가 필요하다.
총 3개다.
- p1이 작을 때 p1 이동하고 p3 이동하기.
- p2가 작을 때 p2 이동하고 p3 이동하기.
- 나머지 안 움직인 p1 또는 p2만큼 넣어가면서 p3 이동하기.
그러면 작은 순서부터 모두 비교한 것을 알 수 있다. 코드 일부를 잘 살펴보자.
while (p1<=mid && p2<=rt)
{
if (arr[p1]<arr[p2])
{
tmp[p3++]=arr[p1++];
}
else
{
tmp[p3++]=arr[p2++];
}
}
while (p1<=mid)
{
tmp[p3++]=arr[p1++];
}
while (p2<=rt)
{
tmp[p3++]=arr[p2++];
}마지막으로 temp 배열 값을 array에 넣어주면 해당 배열에 대한 정렬은 완성되었다고 볼 수 있다. 이를 반복하면 arr 배열에 대한 모든 정렬이 완성된다.
for (int i=lt; i<=rt; i++)
{
arr[i]=tmp[i];
}그럼 완성된 코드를 보자.
소스 코드
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#define MAX 101
using namespace std;
int n;
int arr[MAX];
int tmp[MAX];
void DFS(int lt, int rt)
{
if (lt<rt)
{
DFS(lt,mid);
DFS(mid+1,rt);
int mid=(lt+rt)/2;
int p1=lt;
int p2=mid+1;
int p3=lt;
while (p1<=mid && p2<=rt)
{
if (arr[p1]<arr[p2])
{
tmp[p3++]=arr[p1++];
}
else
{
tmp[p3++]=arr[p2++];
}
}
while (p1<=mid)
{
tmp[p3++]=arr[p1++];
}
while (p2<=rt)
{
tmp[p3++]=arr[p2++];
}
for (int i=lt; i<=rt; i++)
{
arr[i]=tmp[i];
}
}
}
int main()
{
cin>>n;
for (int i=1; i<=n; i++)
{
cin>>arr[i];
}
DFS(1,n);
for (int i=1; i<=n; i++)
{
cout<<arr[i];
}
return 0;
}'C C++ > C C++ 유용한 알고리즘 기법' 카테고리의 다른 글
| DFS - 전위순회, 중위순회, 후위순회 (0) | 2024.11.23 |
|---|---|
| [C/C++] 연속된 숫자 한자리씩 나누어 입력 받기 (0) | 2023.03.16 |
| [C/C++] 배열값 옮기기 (0) | 2022.10.15 |
| [C/C++] 2차원 배열 90도 회전하기 (0) | 2022.10.08 |
| [C/C++] 백준 11653번 소인수분해 (0) | 2022.10.04 |


댓글